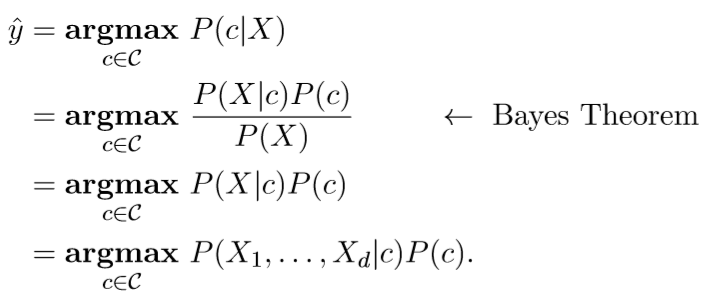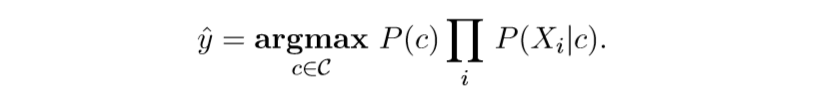前言
垃圾邮件分类是一个典型的二分类问题。我们需要有一系列数据集 其中 $ \mathbf{x_{i}} $ 为邮件包含的内容, $y_{i}$ 为邮件分类的标签,来设计分类器。
1.NB Classifier
1.1最大后验概率判决
直接使用最大后验概率作为判决结果,即建立以下模型
其中 为先验概率,可以很容易的从训练集中估计出来, $P(X_{1},\ldots,X_{d}|c)$ 为需要估计的条件概率。
1.2 Assumption
如果直接估计 $P(X_{1},\ldots,X_{d}|c)$,需要估计的概率为
为了简化模型,我们假设
Assumption1.在给定$c$,即给定邮件类型的情况下,邮件内各个位置的词出现的概率与其余的词无关。
在这个假设下,我们需要估计的概率值大大的减小
但是如果训练邮件数据中篇幅很长,我们依然要估计很多的概率值,使训练实现依然不简单,为此我们引入假设二。
Assumption2.邮件内各个位置出现的词的概率是同分布的。
至此,我们获得了,邮件中每个位置词出现的概率是条件独立并且同分布的。需要估计的概率数量仅为训练数据中出现的不同单词的数量 $\times|\mathbf{c}|$ 。
1.3 概率估计
基于1.2中的假设,我们可以通过以下公式得到需要估计的概率
对于 $c=not\quad spam$ ,也可以通过类似的方式计算。将类别c中的所有单词数记为 $n_{c}$ 类别c中 $w_{k}$ 出现的次数记为 $n_{c,k}$ 那么上式可以些写作
考虑到一般性,垃圾邮件与非垃圾邮件中出现的所有单词不一定会在垃圾邮件的训练集和非垃圾邮件的训练集中都出现。 比如,“word”这个单词在垃圾邮件训练集中出现了,在非垃圾邮件中没有出现,那么 $P(“word”|c=not spam)=0$, 这会影响判决结果的正确性。
因此,我们需要做一个修正
2. Measures
对于二分类器,用混淆矩阵(confusion matrix)来衡量其性能
| label(positive) | label(negative) | |
|---|---|---|
| predict(positive) | TP | FP |
| predict(negative) | FN | TN |
最后附上GitHub:https://github.com/zht1999/NBclassfier