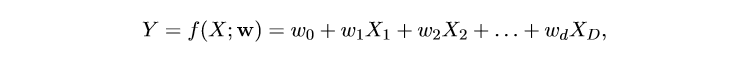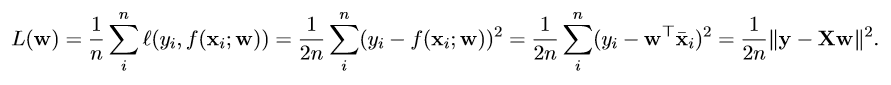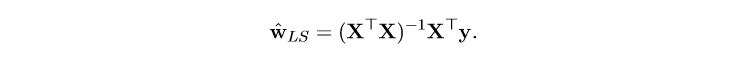前言
对于线性回归问题,我们可以对输入和输出建立如下模型
其损失函数可以表示为
我们通过让损失函数达到最小来求解线性回归问题的最优解。其闭式解为
在数据量非常大的时候,矩阵求逆会占用大量的计算资源,让通过闭式方程求解变得不可行。为此引入梯度下降法。
1.数学原理
1.1梯度下降法
梯度下降法的原理非常简单。若一个凸函数存在最小值,则任意选定一个定义域内的点进行迭代,每步迭代都朝梯度的反方向(函数值下降最快的方向), 随着迭代次数增多,或逐渐逼近最小值点。
其算法实现如下,
为了让梯度下降算法可以更好的收敛到最小值点,需要对迭代步长 $\alpha$ 做一些限制,一般情况下,会取 $\alpha\in(0,1).$
在更严格的数学证明中,可以证明选取
时,梯度下降法可以线性收敛到极小值点。其中 $L$ 为函数的 Lipschitz 常数。
1.2凸函数
线性回归中的损失函数是一个二范数的形式,二范数中是一个仿射函数。根据凸函数的性质可以证明损失函数是一个凸函数。
2.算法实现
2.1数据标准化
在进行训练之前一般会将数据归一化,在例程中使用了极大极小归一化。
2.2选取迭代步长
接下来选取迭代步长
据此选取
矩阵范数即为其最大特征值(matlab中有求特征值的函数,若矩阵可逆,也可以求近似最大特征值)。据此可以获得迭代步长。
tips
训练数据稀疏的情况下,在Matlab中使用稀疏矩阵乘法会更快。
最后附上GitHub:https://github.com/zht1999/GD_regression