简介
通过程序实现C-均值算法对样本进行聚类,了解误差平方和函数的优势与劣势,了解初始代表点的选取对样本聚类效果的影响。
1.原理
定义误差平方准则函数 $J_c=\sum_{j=1}^{c}\sum_{k=1}^{n_j}|x_k-m_j|^2$ ,要使总体的误差平方函数准则函数最小,由于每个样本在分类过程中是独立的,所以要求对于每个样本来说 $|x_k-m_j|^2$ 要最小,这等价于让每个样本的 $|x_k-m_j|$ 最小。那么问题便转换为了寻找C个样本中心点,C-均值算法在选取一组初始中心点的情况下,进行多次迭代并重新计算中心点,直至分类情况不再发生变化
2.实验内容
本次实验中,所采取的产生样本点的方法为使用matlab库函数mvnrnd产生,其中可自定义均值μ,和协方差矩阵Σ产生不同位置以及不同离散程度的服从正态分布的样本集。实验中为了便于控制影响因素和分析并且考虑到泛化能力都采取了三组样本点。
2.1初始点选取方法
试就不同的初始分划,观察集群结果对初始分划的敏感性。在实验中,选取了四种产生初始聚合中心的方法,分别为:
- 顺序选取C个初始聚合中心;
- 随机在样本集中选取C个初始聚合中心;
- 使用密度法选取C个初始聚合中心。以每个样本作为球心,以d为半径做球形;落在球内的样本数称为该点的密度,并按密度大小排序。首先选密度最大的作为第一个代表点,即第一个聚类中心。再考虑第二大密度点,若第二大密度点距第一代表点的距离大于d1(人为规定的正数)则把第二大密度点作为第二代表点,,否则不能作为代表点,这样按密度大小考察下去,所选代表点间的距离都大于d1。d1太小,代表点太多,d1太大,代表点太小,一般选d1=2d。对代表点内的密度一般要求大于T。T>0为规定的一个正数。在本次实验中,选定d=0.5,d1=1,未对T做严格限制。
- 模仿最小最大距离中初始聚合中心选取的办法。选取第一个样本作为第一个聚合中心,第二个聚合中心选取距离第一个聚合中心最远的样本点,第i+1个聚合中心选取与前i 个聚合中心距离最小值中最大的样本点。
实验中产生三组样本点,分别用四种方法产生的初始样本点对其进行聚类。经过多次实验发现,顺序选取和随机选取的方法有不稳定性,聚类结果会随着初始聚类中心产生的随机性而产生时好时坏的结果。若初始聚合中心选取较为合理,如用密度法和最大距离法选取,聚类的结果比较稳定。
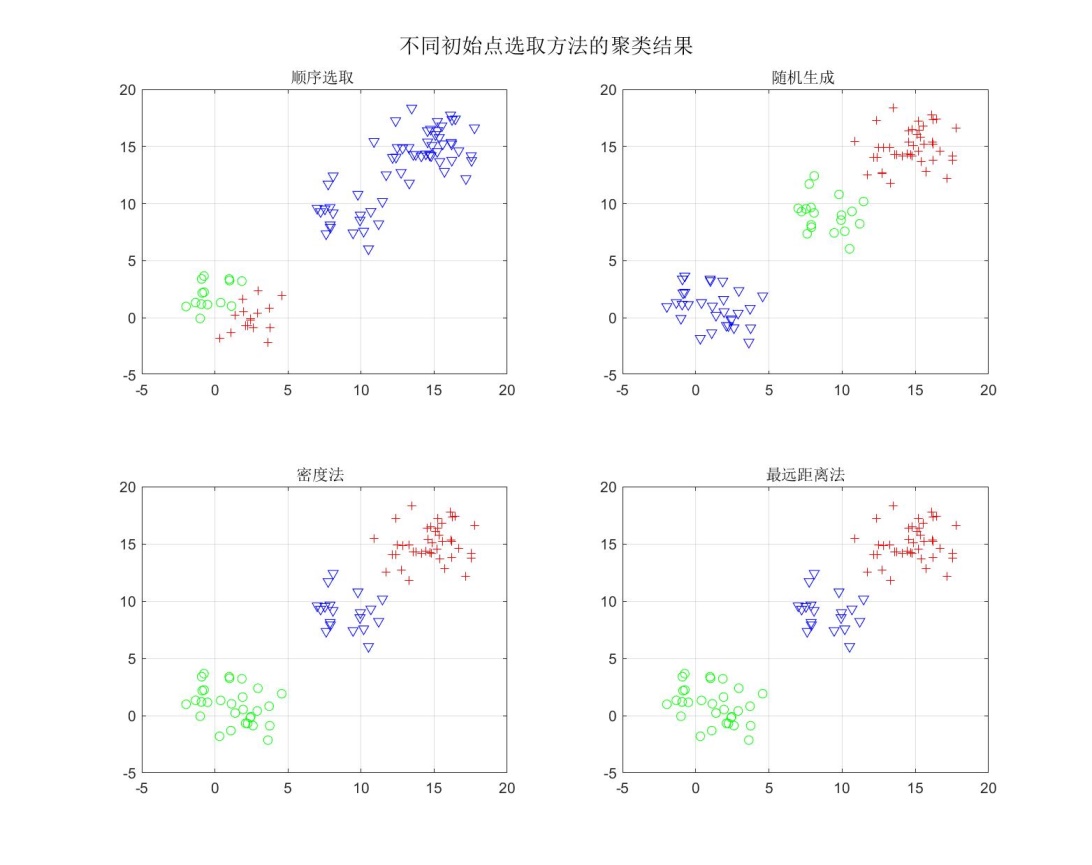
2.2改进聚类准则函数
当各组样本点数目相差不大且分割很开时,聚类效果很好,当样本数目差别很大时,聚类效果很差。经过了多次实验之后,情况依然如此。分析误差平方和准则函数 $J_c=\sum_{j=1}^{c}\sum_{k=1}^{n_j}|x_k-m_j|^2$ ,准则函数中只考虑到了距离的因素,未考虑样本的数目及离散程度,造成了当各组样本点数以及样本点范围随着点数增大而增大时,没有很好的聚类效果。结合实验结果以及理论分析,可以得出结论,误差平方和准则函数适用于各组样本点分割很开并且密集程度差别不大的情况,但不能很好的处理各组样本点数目差别很大的情况。
要改进聚类算法使得其适用于各组样本点数目差别很大的情况,必须要考虑到各组的样本数目和样本的离散程度。可使用加权平方平均距离和准则, $J_l=\sum_{j=1}^c[P_j∙S_j]$ ,其中$P_j$为j类的先验概率,$S_j$为j类中所有样本距离的平均值。在实际的聚类分析中,无法预先知道类别的先验概率,可以根据聚类每次迭代的结果各类的样本数目做先验概率的估计,由于在第一次聚类迭代中,各类的初始数目都为0,无法直接采用当前数目估计先验概率,并且,在开始迭代时可能由于样本输入次序并不是完全随机的使得各类的数目会有较大的误差导致先验概率严重偏离真实值,故采用在误差平方和聚类结果的基础上用加权平方平均距离和准则修正聚类结果的方法。基于以上的思路,在程序实现时,每次对一个样本点进行操作时,先将此样本点从所在类中剔除,再只需计算此样本点分别在各类中与其他样本点距离的平均值,根据最小值所在类确定是否移动,由于剩余样本没有移动,所以无需计算S_j。每次迭代中依然要重新计算聚合中心。 在给定初始样本分布的情况下,用误差平方和准则和用加权平均平方距离和准则修正分别的到的聚类结果如下图所示。
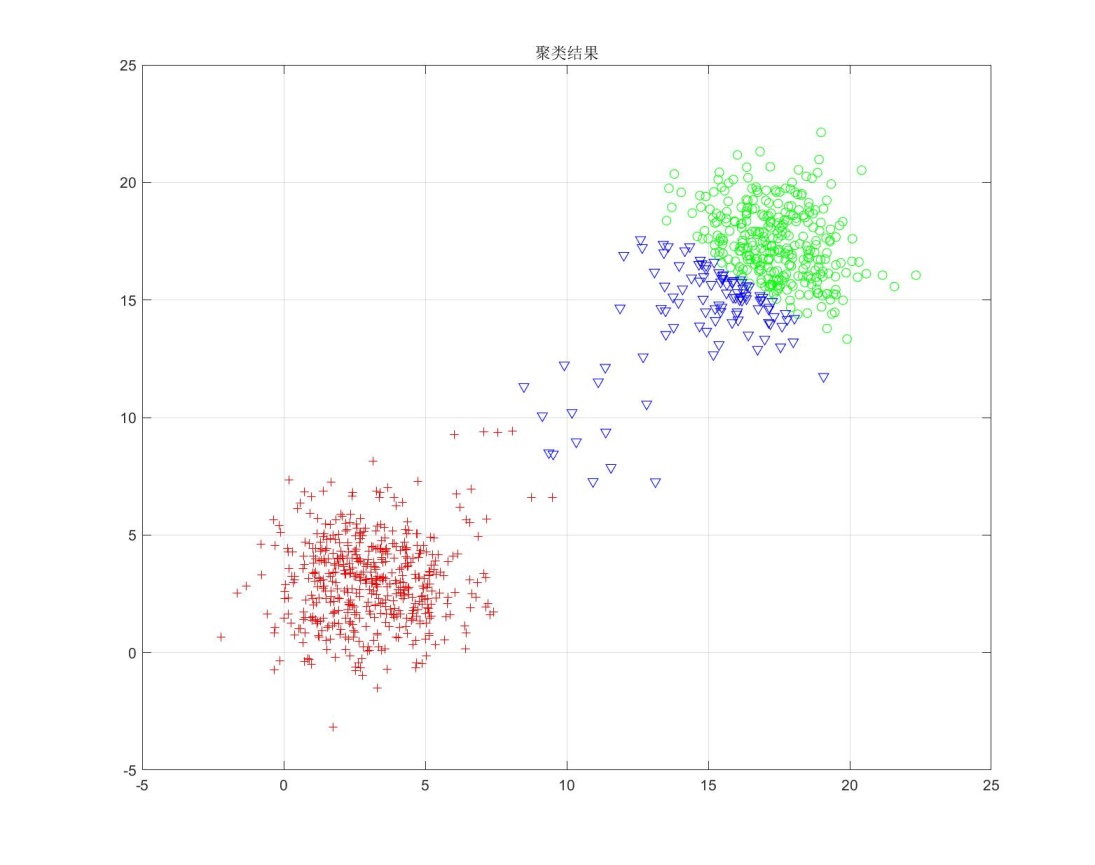
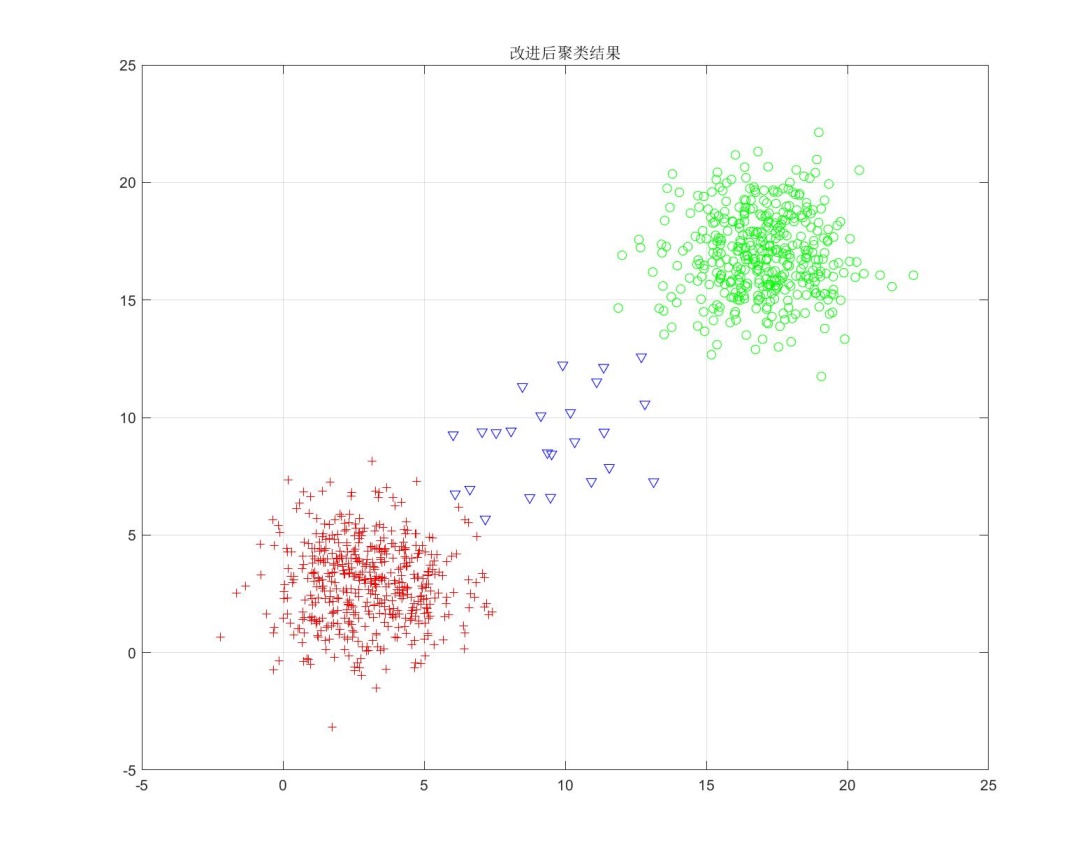
对比改进之前和改进之后的聚类效果,可明显看出改进后的聚类结果与原始样本点分布更接近,表明这样的改进是有效的。
最后附上GitHub:https://github.com/zht1999/C_Clustering