前言
在FFT算法出现之前,用DFT对信号做分析基本上只是理论研究,以当时的硬件技术不能运用到实际中。FFT大大减少了DFT的运算量,使得其成为可能。
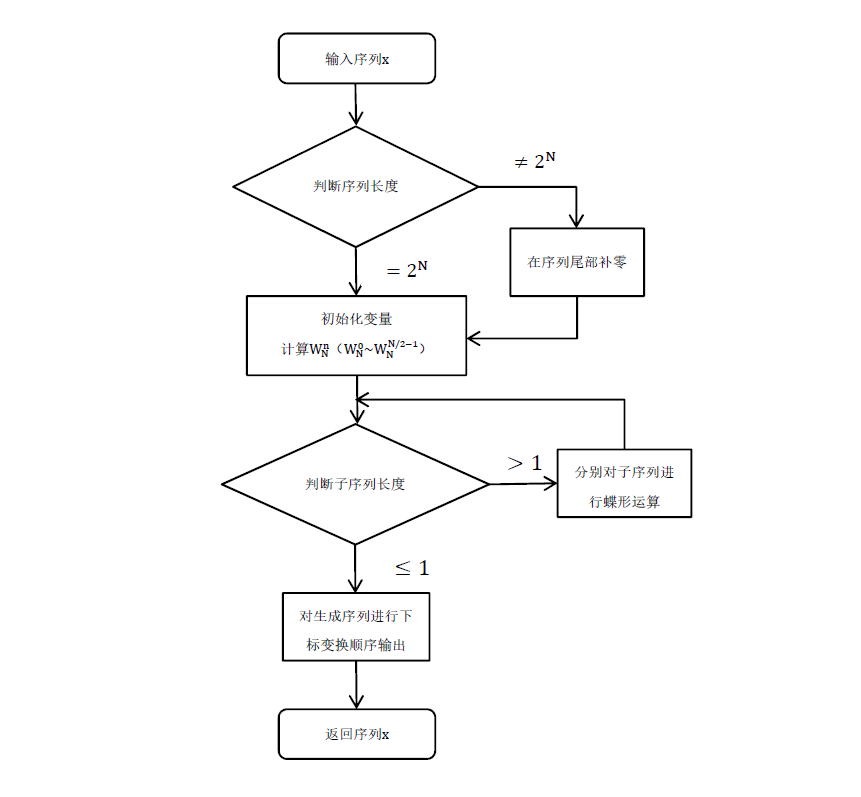
1.算法流程
2.编程技巧
2.1 基2蝶形运算
利用 $W_N^n$ 的周期性和对称性,减少重复计算的次数,将运算的时间复杂度从DFT的 $O(n^2 )$降为 。方法是将原序列分解为两个等长序列,分别做DFT,分解的子序列可以继续分解,直至分解到序列长度为2时停止分解。每次分解做相应的计算。
2.2 对原序列操作
对原序列进行操作,不申请新的内存,会增加少量的时间复杂度,但可以忽略不计。只在原序列内存空间基础上操作,可以节省运算时所需的内存,在有限的CPU资源下,可以对更长的序列进行FFT变换。
2.3 申请额外内存减少重复运算次数
- 思路:在基2算法中,通过蝶形运算已经降低了很大的时间复杂度。但是,在计算过程中仍然会重复使用某些 $W_N^n$ 。基于此,在单次计算中保存之前未得到过的 $W_N^n$,在之后的运算中若重复使用,则直接调用已计算好的 $W_N^n$,这样可以减少计算量。
- 实现:在每次计算过程中,设子序列长度为 $\frac{N}{i}$,那么当计算到第j个蝶形运算时,需要用到 $W_{\frac{N}{i}}^{j-1}$,又由于 $W_{\frac{N}{i}}^{j-1}=W_{N}^{j-1}$,可以根据上标建立一个 $W_N^n$与存储数组的一一映射关系,即 $index= i(j-1)$。
- 改进:
- 由于$W_N^0=1$,所以在计算以及存储时,不需要考虑$W_N^0$,根据判断$index≠0$,可以跳过$×W_N^0$的运算。
- 在对基2算法进行了进一步分析之后得到结论,在计算过程中,$W_N^0~W_N^{N/2-1}$都会用到,故在开始计算FFT前,可以先将其都计算好,在计算过程中可以减少判断次数。
- 根据指数函数的特性,有$W_N^n W_N^m=W_N^{n+m}$,比较直接计算$e^{-iω∙index/N}$与$W_N^n=W_N^{n-1}∙W_N^1$递推公式的速度,在2.的方法下,后者更快。
结合上述三种改进方法可以使的复数乘法的运算次数进一步减少。
3.结果与分析
3.1 时间复杂度
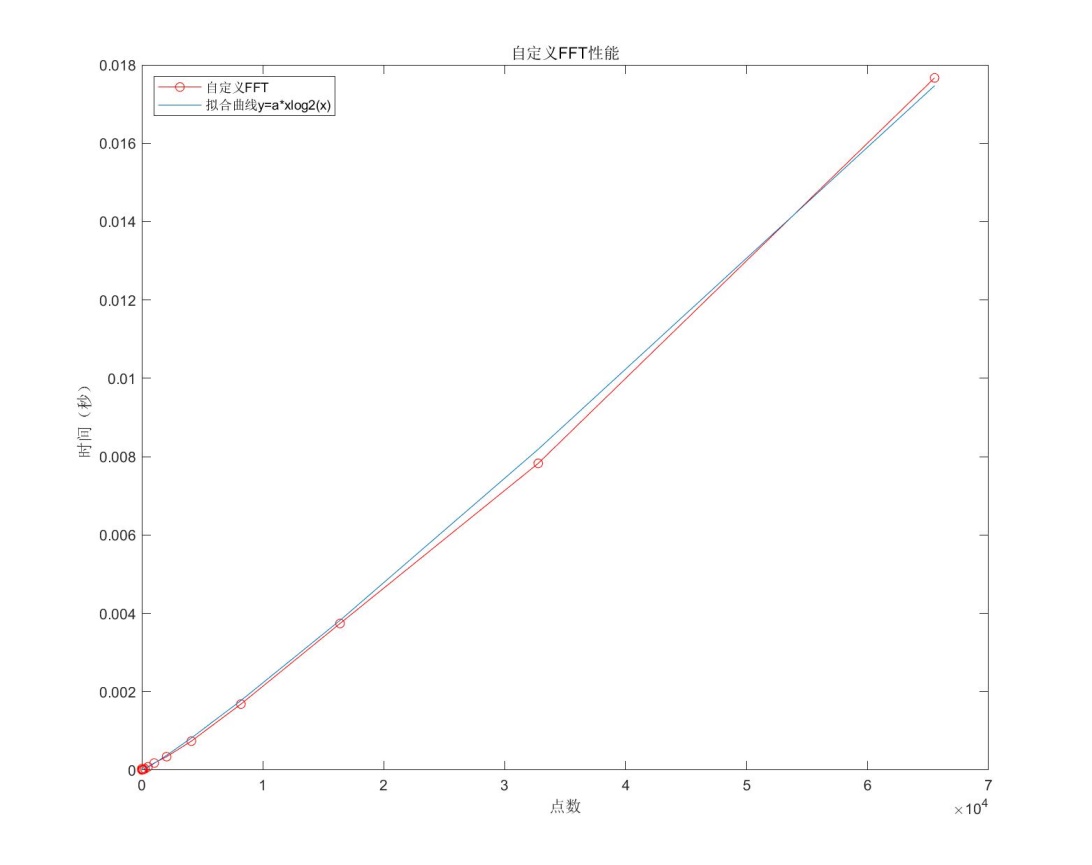
用自定义FFT程序对一序列不同点数情况下各进行20次计算,取均值绘出如下图像。用xlogx函数进行拟合,得到系数a=1.66604489315095e-08。残差平方和为a=1.93194339252435e-07,可以看出,拟合效果很好。
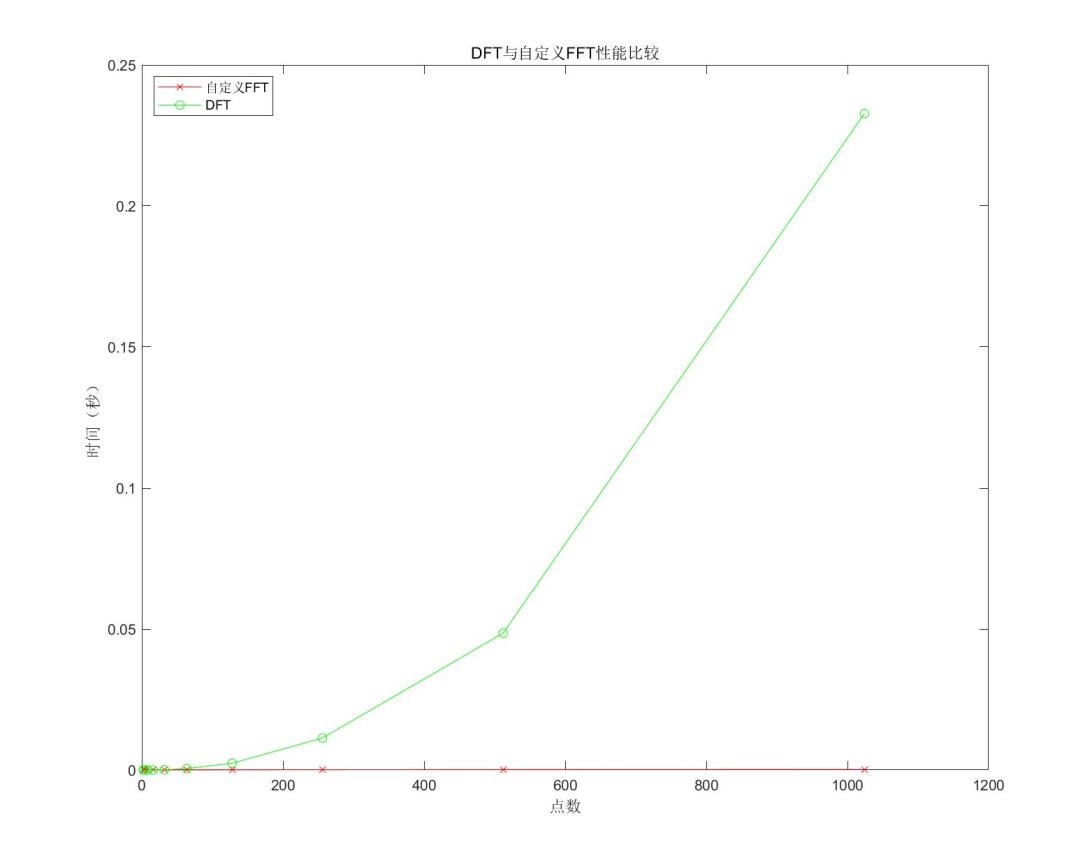
3.2def_FFT vs. DFT
由于实验一中DFT算法不仅有很高的时间复杂度也有很高的空间复杂度,所以在此测试时选取的点数上限较少。测试方法与3.1中相同,可以看出def_FFT用时相比DFT优化了许多。def_FFT的时间复杂度为$O(nlogn),空间复杂度为$O(n)$,而DFT的时间复杂度为$O(n^2)$,空间复杂度为$O(n^2)$。
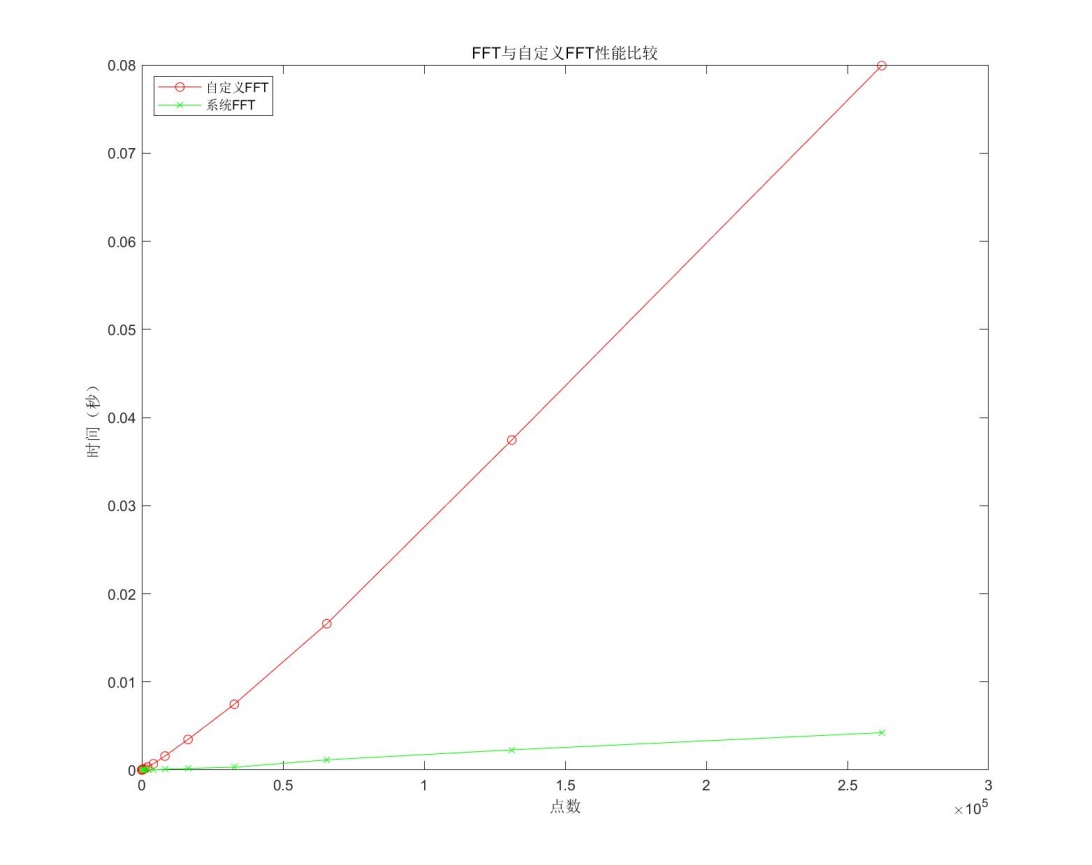
3.3def_FFT vs.系统FFT
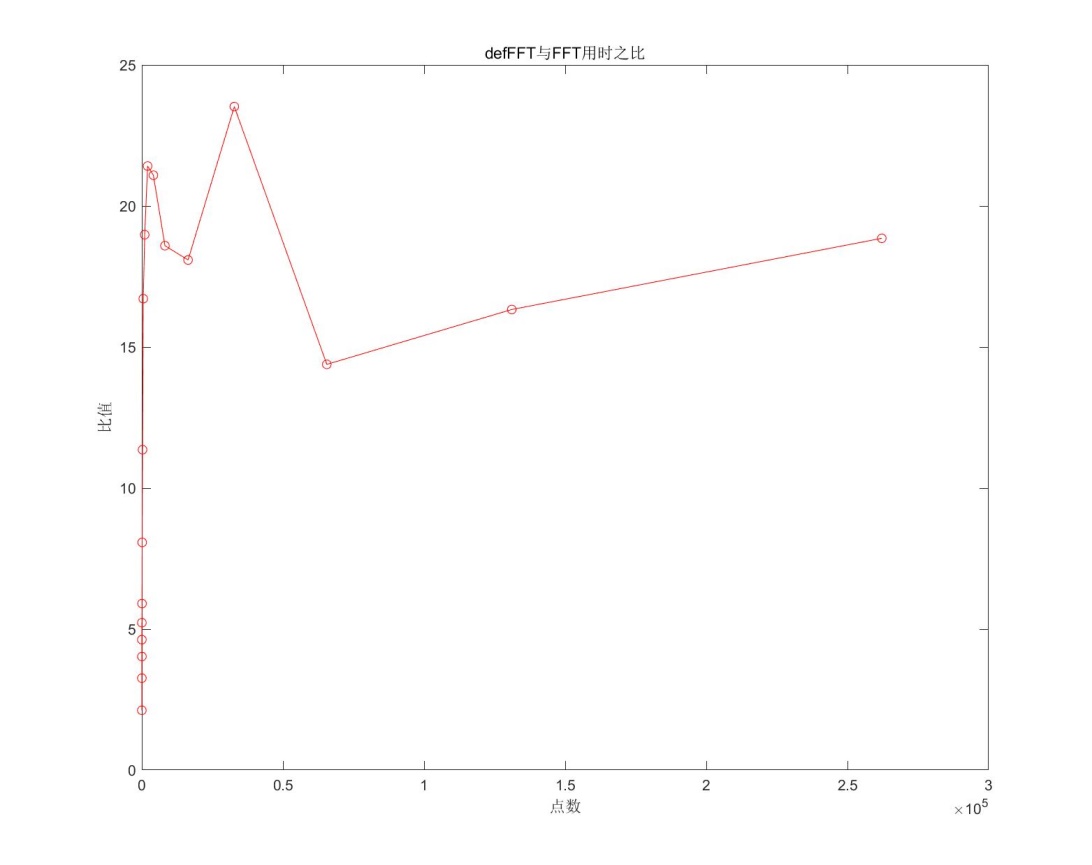
对matlab系统FFT与自定义FFT进行测试,测试方法同3.1。从图中可以看出,自定义FFT比系统FFT用时显然要多。当点数较小时,差异比较小,这主要是因为算法优化在大量加法和乘法计算时才能很好的体现,随着点数增多,自定义FFT与系统FFT用时之比趋于稳定。在不考虑偶然因素的情况下,可以认为,用时之比在10~30倍之间。
最后附上GitHub:https://github.com/zht1999/FFT