基于分治策略和一些处理技巧，Strassen算法的流程如下：
- 两个矩阵A B相乘时，将A, B, C分成相等大小的方块矩阵：
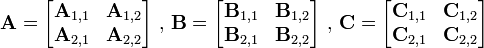
- 可以看出C是这么得来的：
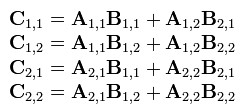
- 现在定义7个新矩阵：
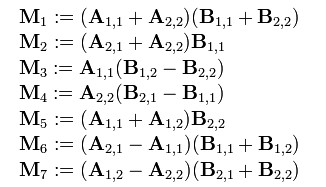
- 而最后的结果矩阵C 可以通过组合上述7个新矩阵得到：
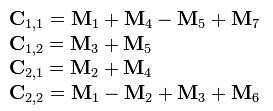如此，通过递归算法，可将N阶矩阵化为二阶矩阵相称。
Strassen算法比通用矩阵相乘算法好一点，因为通用矩阵相乘算法时间复杂度是 ，而Strassen算法复杂度只是 。但随着n的变大， Strassen算法是比通用矩阵相乘算法变得更有效率。
最后附上GitHub：https://github.com/zht1999/Stressen
